Maths

A high-quality mathematics education provides a foundation for understanding the world, the ability to reason mathematically, an appreciation of the beauty and power of mathematics, and a sense of enjoyment and curiosity about the subject.

At Knollmead Primary School, we have adopted a mastery approach in order to deliver the three aims of the National Curriculum, fluency, reasoning and problem solving. Underpinning this pedagogy is a belief that all children can achieve in maths. We believe in promoting sustained and deepening understanding by employing a variety of mastery strategies, with teaching for conceptual understanding at the heart of everything we do. Our approach aims to provide all children with full access to the curriculum, enabling them to develop independence, confidence and competence – ‘mastery’ in mathematics in order to be independent mathematicians who are well equipped to apply their learning to the wider world. 

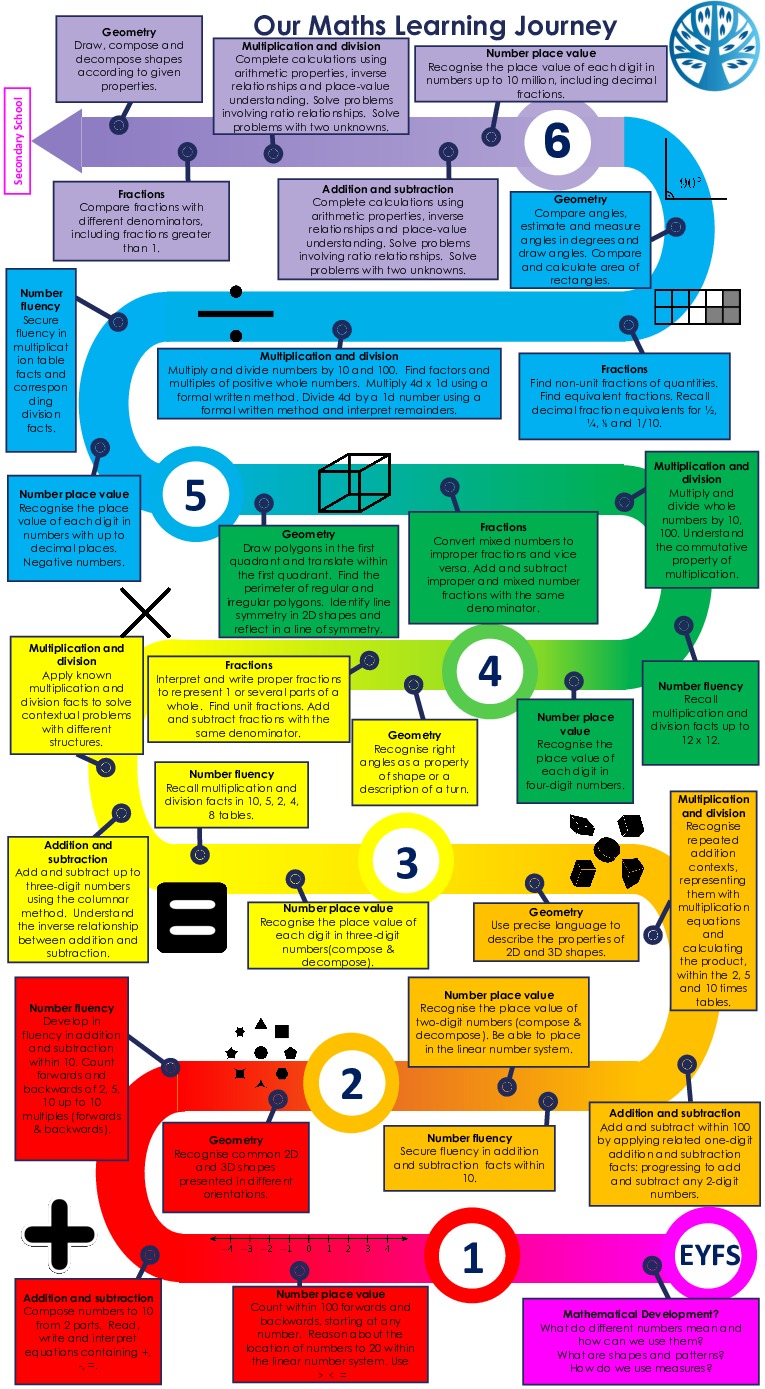
We follow the NCETM (National Centre for Excellence in the Teaching of Maths) Prioritastion Curriculum as a source of planning. Produced by the NCETM and in alignment with DfE guidance, the curriculum prioritises the areas set out in the ‘Ready-to-progress’ criteria.vThis shows each year group what the core concepts are and hence what they need to devote most teaching time to, so that pupils can access new learning in the next school year.

The NCETM curriculum resources support us in our teaching for mastery approach across the school; while we aim to broadly follow their lesson-by-lesson overview, it is adapted to the needs of each class as required.

The NCETM have curriculum maps that show what is covered in each year group at Knollmead.

We believe that the children who require the most support should be taught by the most experienced staff, and as such, in Key Stage 2, some children who are working significantly below their peers are taught each day by the Senior Leadership Team. The children follow the same curriculum but spend longer on key areas of learning to support ‘overlearning’ and mastery, supplemented with a greater daily focus on the development of fluency of number, to support pupils to work with and understand concepts by reducing demands on working memory.

Our maths leader is Mr Tan, who was also headteacher advocate for Kingston Upon Thames for the London South West Maths Hub providing support for headteachers in four local authorities in leading whole school change through lesson study between 2020 and 2022.

Please see the video examples below of how to support your child learn their times tables:

Modelled by an adult and then the child copies. To reduce the cognitive load, only the first 6 times tables are introduced.

It is important here that the child also uses their fingers to support the skip counting. This allows them to build on their times tables from 5 x ? (the fifth finger) as they learn more facts

The child copies the teacher as they cover a new multiplication fact. The process of skip counting uses constant repetition and encourages children to pronounce the facts clearly to further embed them into their long term memory.

The child is now encouraged to say the times tables out loud in order. The process of skip counting has been removed and saying (chanting) the times tables facts is introduced. The use of a tennis ball is encouraged to make the activity fun.

The chanting, or retelling of multiplication facts is now repeated but backwards. Once again the child has to say the full times tables facts, plus answer to further embed the facts in their long-term memory.

Once again the child is to say the whole multiplication fact and answer, but this time the order is randomised and the teacher dictates the questions. As the child grows in confidence division calculations calculations are also introduced. Just like in clips 5 and 6 the child does this activity using the tennis ball.

This child is now encouraged to use the multiplication facts to answer questions using the times table practice. The calculations that the child is asked to solve are made more challenging by not always asking for the missing answer, but for part of the calculation also.

The child is encouraged to use the 'distribution law' to further understand times tables. For examples 5 x 8 + 2 x 8 = 7 x 8. They could learn to solve this as seen below

5 x 8 = 40

+ 2 x 8 = 16

7 x 8 = 56